Recap
In the first post of this series, I walked through the basic ideas of what constitutes a graph, and in the second post I discussed a particular kind of graph called a directed acyclical graph (DAG), providing a handful of examples from the world of data engineering along with an attempt to disambiguate – and expand – the meaning of what a DAG is.
To briefly recap the important points discussed in the posts so far:
- A graph consists of one or more nodes.
- Nodes are related to other nodes via one or more edges.
- Nodes that that can reach themselves again (in a single direction) indicate the graph has a cycle.
- A given edge can be directed or undirected.
- Nodes and edges can have attributes, including numerical attributes.
- Graphs without cycles, with only directed eges, are called directed acyclical graphs (DAGs).
- Hierarchies are DAGs in which each node only has a single predecessor node.
In the following post, we’re going to discuss hierarchies in detail. We’ll discuss a few examples, address a few additional attributes that emerge from the definition of a hierarchy and we’ll introduce an initial data model for hierarchies.
Hierarchies
As indicated in the last post and summarized above, a hierarchy can be thought of as a DAG in which any given node has a single predecessor node (except for the root node, which of course has no predecessor.) Given this constraint, its incredibly common to refer to predecessor nodes as “parent” nodes (despite only having one such predecessor node, and not two as the analogy would otherwise indicate. Such analogies are, of course, frequently imperfect). Similarly, successor nodes are frequently referred to as “child” nodes. We’ll stick with this “family” naming convention for the rest of the series, given its utility but also its wider adoption with BI vernacular.
(Note: despite this “ideal case” definition of child nodes only having a single parent node, there are indeed edge cases where a node can potentially have more than one parent, but such cases are the exceptions, and they need to handled on a case-by-case basis. Perhaps in a future post I’ll spend time discussing these cases in more detail, but for our purposes, and in light of the expected cardinality of dimensional modeling (i.e. many-to-one from fact table to dimension tables), we’re going to move forward with the expectation that any/all hierarchies should always respect this relationship, i.e. a child node only ever having a single parent node.)
Also, as alluded to in the last summary point of this post, hierarchies can be considered a kind of “tree” data structure (a directed rooted tree, more specifically), which is a formally defined data structure from graph theory. While graph theory is rarely invoked in discussions of business intelligence, it is important to note that the tree analogy does indeed carry over, with terms like “root nodes”, “branches” and “leaf nodes” frequently used, which we’ll discuss later. (Don’t you love mixing metaphors? Family metaphors. Tree metaphors. Family trees anyone?)
So, here’s a basic visualization of a hierarchy:
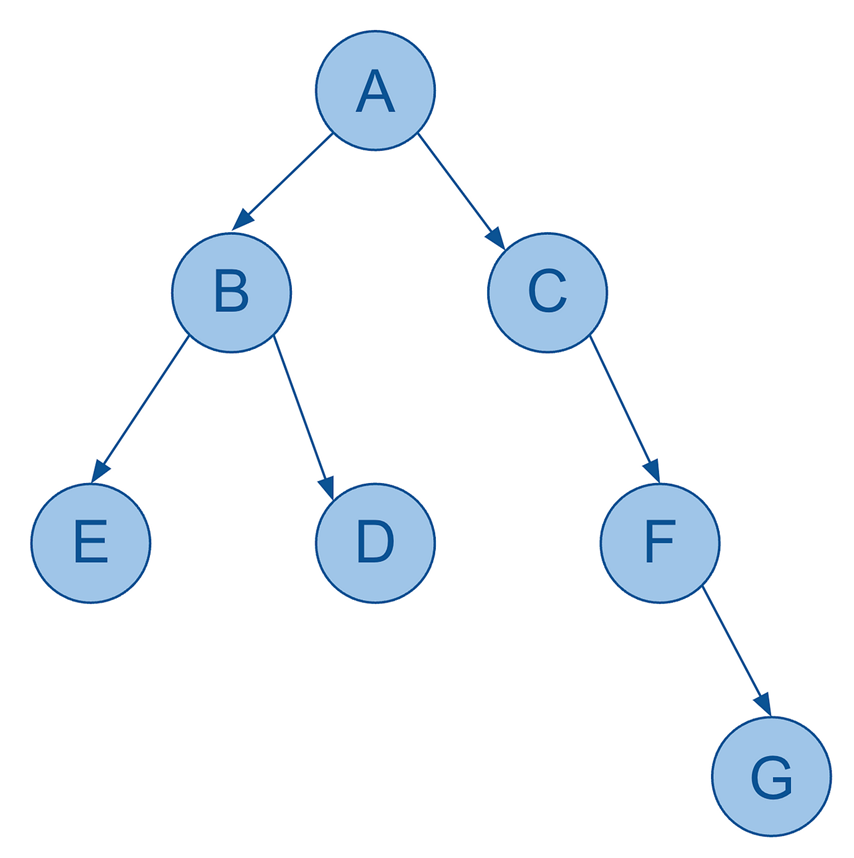
As you can see, it’s still very much a graph (and indeed a DAG) with:
- seven nodes
- six edges (directed)
- no cycles
- each node only has a single parent
So far so good.
I mentioned earlier that even though hierarchies have more constraints, i.e. they’re more limited in what they can represent compared to generic graphs, they nonetheless yield additional attributes. What do I mean by that?
Consider the following two points.
Firstly, because I have:
- a single starting point (i.e. the very first parent node),
- only directed edges,
- no cycles,
a hierarchy therefore allows me to measure the “distance” of any node in the hierarchy by how many edges away from the starting node (or “root node” as we’ll later call it) it is. This measurement is typically referred to as which level a particular node is on (analogous to measuring how high up in a building you are by what level you’re on. And much like the British/American confusion around which floor constitutes the “first” floor, you’ll also have to decide whether you index your root node at level 0 or 1, although 0 is more common).
Note that level is a value that can be derived from the data itself, and thus is slightly redundant as its own column – but such derivation introduces unnecessary complexity and potential performance headaches, and thus benefits from being persisted as part of transformation logic in a data pipeline.
Also note that this level attribute can be considered a node’s “natural” level, but that business requirements may dictate treating a node as though it has a different level. A more detailed discussion on such cases can be found in the 5th post of this series, where unbalanced and ragged hierarchies are addressed.
It’s also worth noting that you can, of course, measure the number of edges between any two nodes in a generic graph, but unlike with hierarchies, there’s not a single value for level per node but rather N-1 such values, i.e. since you can measure the number of edges between a given node and all other nodes in the same graph. Storing such information for all nodes introduce exponential storage requirements, i.e. O(n²), and offers very little technical or business value. Hence level is a fairly meaningless attribute in the context of generic graphs or DAGs.)
Secondly, because you can now refer to multiple “sibling” nodes under a single parent, you can describe the sort order of each sibling node. In other words, you define a particular sort order for all the related sibling nodes under a particular parent node. (This is another example of an attribute that is meaningful for hierarchies, but really doesn’t make much sense in the context of a generic graph or DAG.)
A classic example of this are the various lines in a financial statement such as a profit-and-loss statement:
Financial reports are a very common use case in the world of BI, and it’s clearly extremely important to ensure that your reports display the various lines of your report in the correct order, defined by the sort order of each node in your financial statement hierarchy. (Note in the image above how this sort order is defined at each level.)
It’s worth noting that this sort order attribute doesn’t have a canonical name in the world of BI as such. But for a variety of reasons, my preference is “sequence number” (SEQNR as its column name), so we’ll stick with that for now.
(Also, for folks new to hierarchies, you might find it a worthwhile exercise to analyse the financial statement structure above as a hierarchy: How many nodes does it have? How many edges? How many levels? How many child nodes per parent? How might you actually model this data in a relational format? We’ll come back to this in a bit…)
Two more points I’d like to make, as we work towards a generic/reusable data model for hierarchies:
- This should be obvious, but there are many different types of hierarchies, such as (in an enterprise context): profit centre hierarchies, cost centre hierarchies, WBS structure hierarchies, cost element hierarchies, financial statement hierarchies, and the list goes on.
- A particular hierarchy type might have multiple hierarchy instances. For example, a time dimension is actually a hierarchy, and almost all large enterprises care about tracking metrics along both the calendar year as well as the fiscal year, each of which is its own hierarchy. (We’ll circle back to time dimension hierarchies here in subsequent posts.)
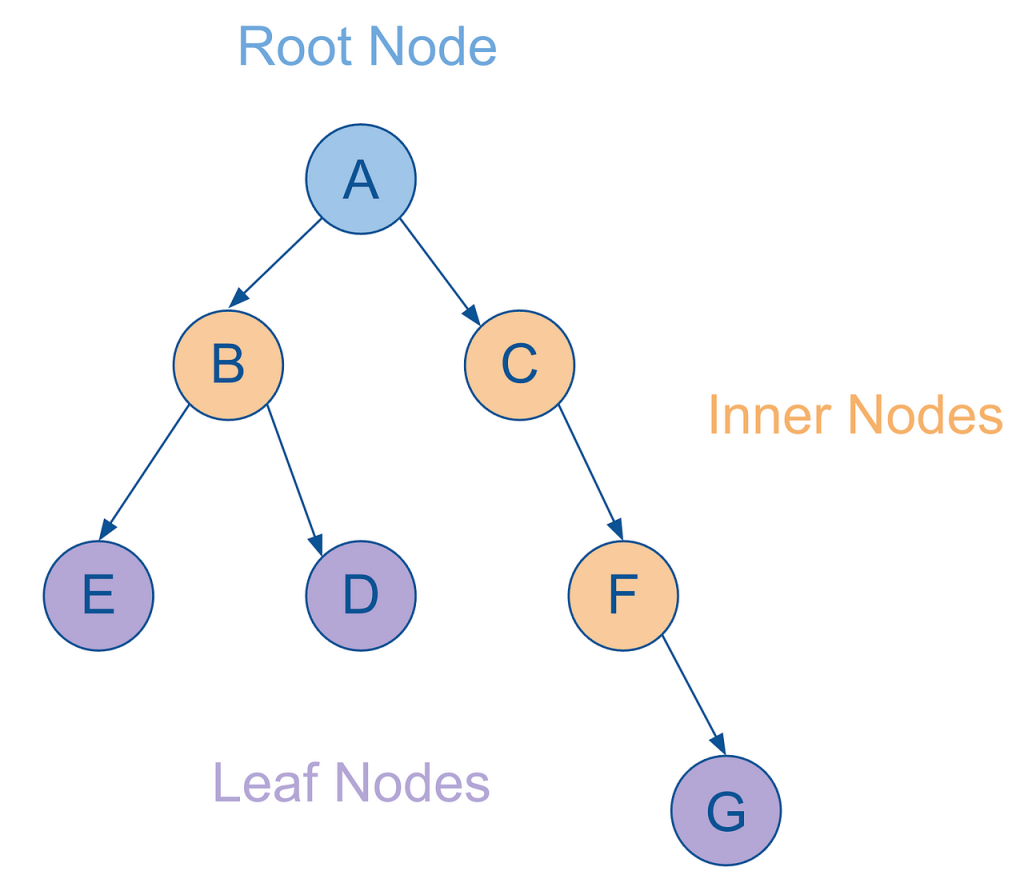
And lastly, let me introduce a bit more vernacular from the tree analogy introduced earlier:
- As mentioned above, a given hierarchy has one root node
- Any nodes that have parent and child nodes are called intermediate or inner nodes.
- Any nodes that have parent but no child nodes themselves are called leaf nodes.
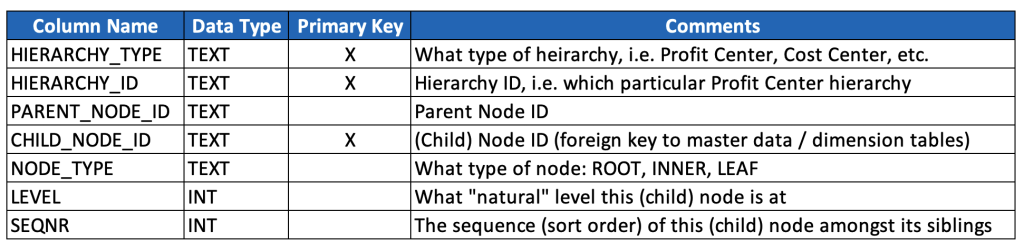
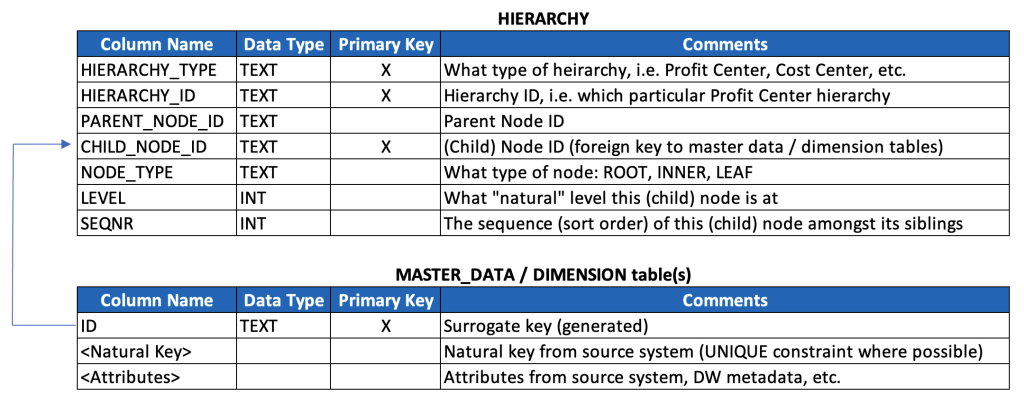
Ok, let’s now look at a basic, generic and reusable data model for storing hierarchies. This is the beginning of the discussion, and not the end, but it gives a strong foundation for how to accommodate many different types and instances of hierarchies.
Rather than write the SQL, I’m just going to provide a poor man’s data dictionary, especially given that your naming conventions (and probably also data types) may well differ. (For a detailed review of SQL that may help you ingest and model hierarchies, see the 6th post in this series.)
Here’s what the example hierarchy above would look like in this model (primary key fields highlighted):
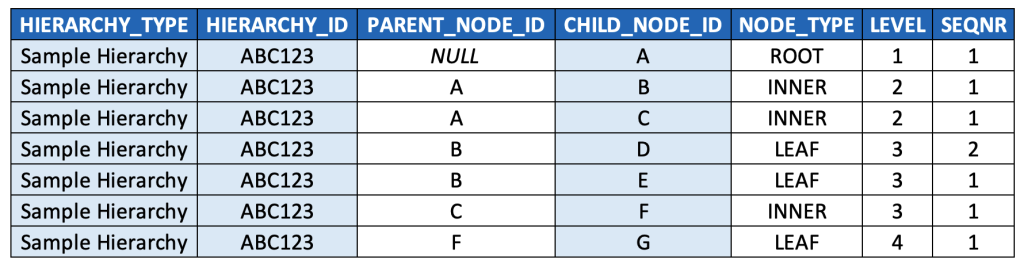
It’s worth taking a moment to talk through this a bit.
- First of all, I’d suggest playing with some sample data, and sorting by the different columns, to familiarise yourself even more with this data model. For example, you could sort by NODE_TYPE to quickly find all the INNER nodes and LEAF nodes. You could sort by LEVEL and then SEQNR to “read” the hierarchy as you would with its visualised equivalent, i.e. top-to-bottom, left-to-right.
- Note that root nodes are defined as those records for which PARENT_NODE is NULL. This is a commonly accepted convention, especially for query languages that can parse parent-child hierarchies natively (such as MDX, which we’ll come back to), so I’d highly suggest adopting it (especially if you’re modeling in a strictly OLAP context), but there’s clearly no “formal” reason, i.e. from relational theory or anything else, that requires this.
- If this were a data model for a generic graph or even a DAG, we would have to include PARENT_NODE as part of the primary key, since a node could have more than one parent (er, predecessor). However, since hierarchy nodes only have a single parent node, we don’t need to do this, and in fact, we don’t want to do this (as, from a data quality perspective, it would let us insert records with multiple parent records, which breaks the definition set forth previously for hierarchies, and could lead to incorrect results in our BI queries by inflating metrics when joining hierarchies to fact tables due to M:N join cardinality instead of M:1).
- Be aware that the child nodes in a hierarchy are often just referred to as “nodes”, whereas parent nodes are always referred to as parent nodes.
- SEQNR might be a bit confusing at first glance, because again, it only defines the sort order for a given node compared to its immediate siblings (again, consider the financial statement hierarchy structure that we glanced at earlier. Revenue has to always come before Expenses at the top level, but underneath revenue, it’s important that its constituent child records are also displayed in the right order according to accounting expectations, i.e. “License” coming before “Support”). Now, sorting data only requires that sequential values are larger than previous values, so you could technically use a typical contiguous sequence for this column, i.e. each record in the table increasing by 1, which would give us 1, 2, 3… up to 7. But that kind of implies that all of the records are somehow related to each other when it comes to sorting (which they’re not — sort order only makes sense amongst sibling nodes). So it’s recommended that you restart your sequence for each set of siblings nodes.
- Speaking of sorting hierarchy records — in many cases, such as with GL Account hierarchies, the sort order is defined by the business in a dedicated column, and almost always used in any reporting. However, in other cases, a sort order doesn’t really matter. Think of a typical org chart. If you were looking at expenses charged per department (or employee), you often don’t really care about sort order of the hierarchy, as long as the data is grouped properly (i.e. you can see all of the employees per department, all departments per division, etc.). And lastly, you often only care about the alphanumeric sort order, such as with your time dimension. We’ll get to the time dimension shortly, but it’s absolute a hierarchy in the strict definition, and you’re almost always going to sort your days by their intrinsic value (assuming you have your days modeled properly, i.e. don’t forget your padded zeroes for any columns you use for sorting! Otherwise the value 11 might come before the value 2. The formally recommended way to handle this risk in time data is to model time following the ISO 8601 standard, just FYI.)
Before I forget to mention, you might hear this structure referred to as an “adjacency list”, which is another technical term from graph theory. Technically, an adjacency list maps a single node to all of its adjacent nodes (i.e. within a single record, which you could accomplish with an ARRAY or JSON column), so in the case of hierarchies, a single row would show a parent node maps to *all* of its children nodes (in an array, for example). In practice though, folks often refer to the parent/child data model above as an adjacency list, even though each child node gets its own row. Just FYI.
In Summary
We’ve now gone through graphs, DAGs, and hierarchies, and we’ve walked through a basic, scalable data model for parent-child hierarchies and discussed some of the nuances of this model.
In the next post, we’ll review a few more considerations when it comes to data modeling, such as:
- Discuss data quality implications of hierarchies.
- Disambiguate some confusion around terms like “parent/child”
- Discuss two major patterns for consuming hierarchies, i.e. schema-on-read compared to schema-on-write.
- The reason hierarchies are so prevalent in BI in terms of how human cognition goes about processing information.
